Topological quantum phase transition and quantum magnetism simulation are the frontier researches in the field of ultracold atomic physics. Changing a certain parameter of multi-particle systems when under the absolute zero degree, such as the coupling strength, the pressure or the external magnetic field strength, the system can be continuously changed from one ordered state to another. Since the thermodynamic fluctuations are as important as the quantum fluctuations when at the critical point, this kind of phase transition is completely different from the thermodynamic phase transition induced by temperature and is called as the quantum phase transition. But when under the absolute zero degree, another kind of quantum phase transition may also exist in a quantum system. This special kind of quantum phase transition process does not exist of spontaneous symmetry breaking of Landau theory and the behavior is determined by the bulk properties of the wave function for the ground state of the system. The system is in disordered phases at both sides of the phase transition point and there is no localized order parameter to describe or distinguish the two phases. But a non-localized order parameter may exist and this kind of quantum phase transition is called as topological quantum phase transition [1]. For example, the phase transition between the conductance quantum platform in the fractional quantum Hall effect is a typical topological quantum phase transition.

    However, the manipulation of the parameters of quantum phase transitions in condensed matter physics is very difficult. We can achieve this by using quantum gas in an optical lattice to study the quantum phase transition mechanism and discover novel quantum phase transitions even the implementation of novel states.

    For the two-component bosons or fermions in optical lattices, tag them with the pseudospin variable ↑ and ↓ and interaction U≫J. Using the two order perturbation theory of the kinetic energy term, we correspond the Bose-Hubbard model to the Heisenberg model which has the equivalent spin-spin interaction between adjacent lattice sites,

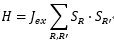
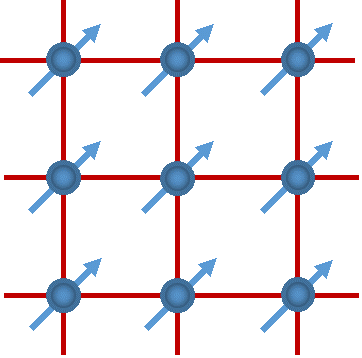
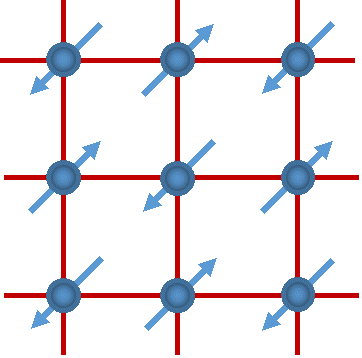
    The sign + (-) of the superexchange coupling strength<span "="" style="font-size: 12pt;">Jex represents fermions (bosons) situation [2], therefore makes the system tend to be antiferromagnetic (ferromagnetic) order.

 

FIG.2 The principle diagram of the superexchange interaction [3]

    The superexchange interaction is the basis for the formation of the quantum magnetic properties in strongly correlated electronic media. The control of the equivalent spin-spin interaction between adjacent lattice sites is also a new way of quantum magnetic simulation. This interaction results from the "virtual" jump between adjacent lattice sites: a particle jumps to adjacent sites, a same particle (or a particle in adjacent sites) jumps back to where it was originally in the lattice at the same time [4]. For the double-spin polarized fermions, such a jump is inhibited by the Pauli exclusion principle. Therefore, two particles of opposite spin can jump and cause a reduction in the total energy of particles.

Ultracold quantum gases in optical lattices

      An optical lattice is typically formed by two interfering laser beams, giving rise to a periodic intensity pattern which is seen as a periodic potential by the atoms. In the optical lattice potential well, the atoms can be trapped in the strongest or weakest position of the laser intensity due to the optical dipole forces arising from the AC Stark effect: If the light field is red-detuned (light frequency smaller than atomic transition frequency) the atoms will be drawn to the intensity maximum, provided they are in the ground state; A blue detuned light field repells the atoms to dark regions.

 

 

      One key motivation for the work with ultracold atoms in the optical lattices is the similarity to solid state systems. The appropriate choice of atomic species and lattice spacing and depth allows to enter the typical parameter regime for solids and to explore condensed matter phenomena in a controlled and almost pure environment. One highlight certainly is the search for the mechanism behind high-temperature superconductivity by exploring the Fermi-Hubbard model and the mechnisms of superexchange interactions.
 

    Full dynamical control over the individual laser-beam intensities as well as over the relative phase between the two standing waves forming the lattice allows us to set all relevant parameters of the atomic many-body system. We obtain87Rb Bose-Einstein condensates with the temperature of 30nK by magneto-optical trap and forced evaporative cooling in optical dipole trap, then load the condensates into a three-dimensional optical lattice formed by three standing wave laser beams. FIG.9 is the material wave interference pattern of the quantum phase transition from the superfluid state to the Mott insulating state we obtained in the three-dimensional optical lattice. FIG.10 is the quantum Newton’s cradle formed by using one-dimensional Bose gases.

 

Summary of experimental system

      The experimental vacuum system is composed of scientific cavity, two dimensional magnetic optical trap, atomic source and ion pump, as shown in Figure 11. The science chamber vacuum is 3×10-9 Pa and the two-dimensional magneto-optical trap cavity vacuum is 3×10-7 Pa. The science chamber is drum shaped, including eight 2.75-inch windows, sixteen 1.33-inch windows and two 8-inch windows in up and down direction. These two 8-inch windows are close to the center of the chamber, for future experimental realization of in situ detection with large numerical aperture.

      Neutral 87Rb atoms are composite bosons with 87 nucleons and 37 extranuclear electrons, the natural abundance is 27.8% (also a stable isotope85Rb accounted for 72.2%), the nuclear half-life is 4.88×1010 years, considered to be stable in usual conditions.
 

      87Rb atomic nuclear spin I＝3/2, ground state 52S1/2 splits into two hyperfine levels, F＝1 and F＝2 respectively, the division of space between them is 6.835GHz, which is used as rubidium atomic frequency; the first excited state 52P3/2 splits into F=0, 1, 2, 3 four hyperfine levels. The transition between them is called as 87Rb D2 atomic line transition. Figure 12 shows the87Rb D2 line hyperfine structural details; Figure 13 is the laser system.

 

      The optical dipole trap is generated by the interaction between the light field and the atomic dipole moment. The typical depth is below millikelvin. Due to the optical dipole trap laser usually are far detuned laser, the excited probability of atoms in an optical dipole trap is very low. Thus the optical dipole trap is very useful as neutral atoms trap, and further by evaporative cooling method of quick access to Bose-Einstein condensates.