1.小型钙原子光钟研究背景
原子钟是目前为止产生最准确时间频率的设备,被广泛运用在全球卫星导航、守时授时同步等系统中,任何需要高精度时间频率的体系基本都离不开原子钟。目前性能最好的原子钟(光频原子钟)准确度和稳定度已进入10-19量级[1],如此优异性能的原子钟正逐渐被运用在精密物理测量、天体物理观测等方面[2,3]。但是光晶格原子钟和离子光钟的应用范围受限于其体积大、系统复杂的特点,我们小组致力于小型钙原子束光钟的研究,采用热原子束源作为量子频率参考,不需要复杂的激光冷却与陷俘等物理结构(包括真空物理结构和激光器等), 物理部分的体积被很大程度的缩小。
小型钙原子束光钟主要研究目标是使具有优异性能的光钟小型化、集成化、可搬运,该研究在确保光钟优异性能(稳定度和准确度)的同时,扩宽光钟的应用范围与场景,使光钟在全球卫星导航系统、守时授时系统、空间光钟、地面光钟网络系统、地球物理天体物理观测、精密物理测量等领域得到广泛的应用,该研究具有重要前景和重要意义。
2.小型钙原子光钟实现方案
相比于传统的直接探测钟跃迁谱线的方法[4],于2006年,我们小组提出了运用于热原子束的转移探测方案[5],该方案极大提高了探测钟跃迁谱线的信噪比,其也被广泛运用在以后的热原子束光钟中[6-9]。于2016年,我们小组报导了自评估的小型钙原子束的光钟,其秒级稳定度为3×10-14,200 s积分时间后其不稳定度下降到3×10-15[7]。于2017年,我们小组实现了基于全密封钙束管的小型钙原子束光学频率标准,并进行了两套系统的比对,1600 s的积分时间后其稳定度为1.8×10-15[9]。
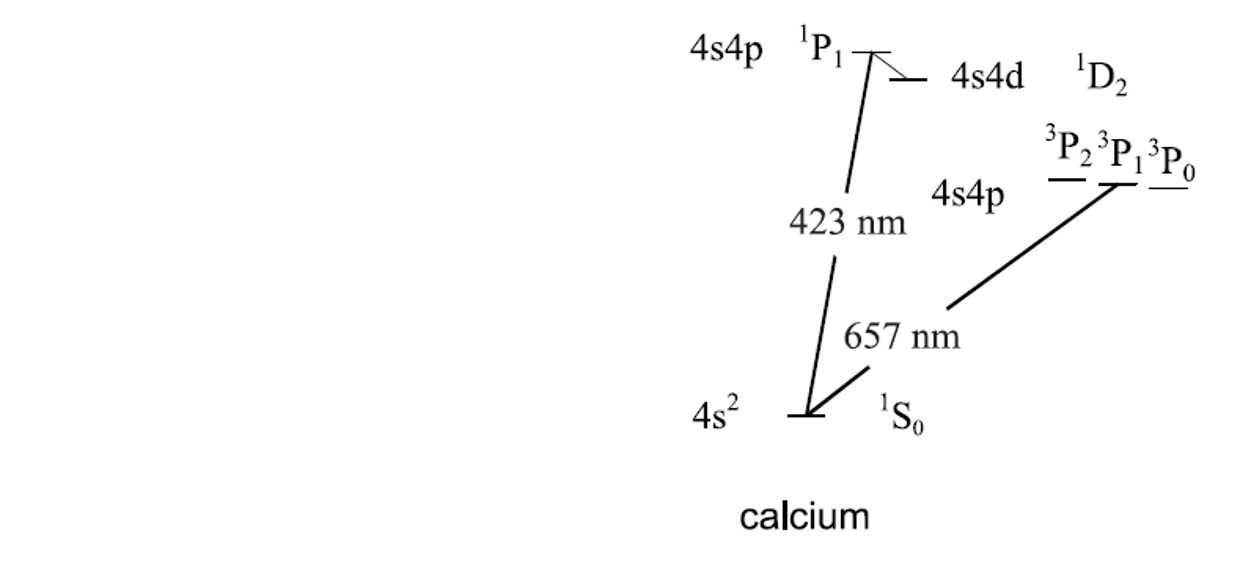
图 1 钙原子相关能级图
图1是钙原子(40Ca)的相关能级图, 我们采用的钟跃迁谱线为1S0-3P1的657nm跃迁,其中亚稳态3P1态的能级寿命为0.4 ms(自然线宽为400 Hz),自发辐射时间较长,直接探测该跃迁谱线的方法受限于收集该自发辐射荧光的效率,不能获得很好的信噪比。我们小组于2006年提出应用于热原子束的转移探测方案[5],即引入1S0-1P1的423nm跃迁,其中1P1态的能级寿命约为4.8 ns,通过423nm的循环跃迁探测与钟激光相互作用后原子基态布居数的变化,从而可以获得1S0-3P1态的跃迁原子数量随钟激光频率失谐量的变化关系,获得的钟跃迁谱线如图2 所示。
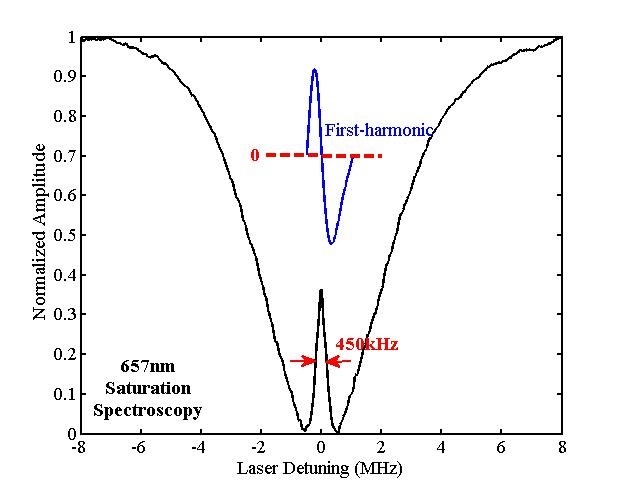
图 2 657 nm钟跃迁谱线(黑色实线)。误差信号(蓝色实线)。
图3所示是我们小型钙原子束光钟的实物图,整个光学部分(不包括Pound-Drever-Hall 系统部分)是被单独构建在一块面积90 cm × 60 cm的光学面包板上,并被密封在一个黑色的盒子里,减小气流的扰动和外界杂散光的干扰。整套系统只采用了两台光栅外腔半导体激光器,一套作为量子参考的热原子束管,一套超高精细度的光学谐振腔。

图3 小型钙原子光学频率标准实物图
为了进一步推进小型化与可搬运特性,我们采用了体积更小、鲁棒性更好的全密封型钙束管,其更有利于可搬运特性。目前我们已经实现了基于全密封钙束管的小型钙原子束光学频率标准,并进行了两套光学频率标准的比对。如图4所示,是我们两套光学频率标准比对后的稳定度数据,1600 s的积分时间后稳定度为1.8 × 10-15。
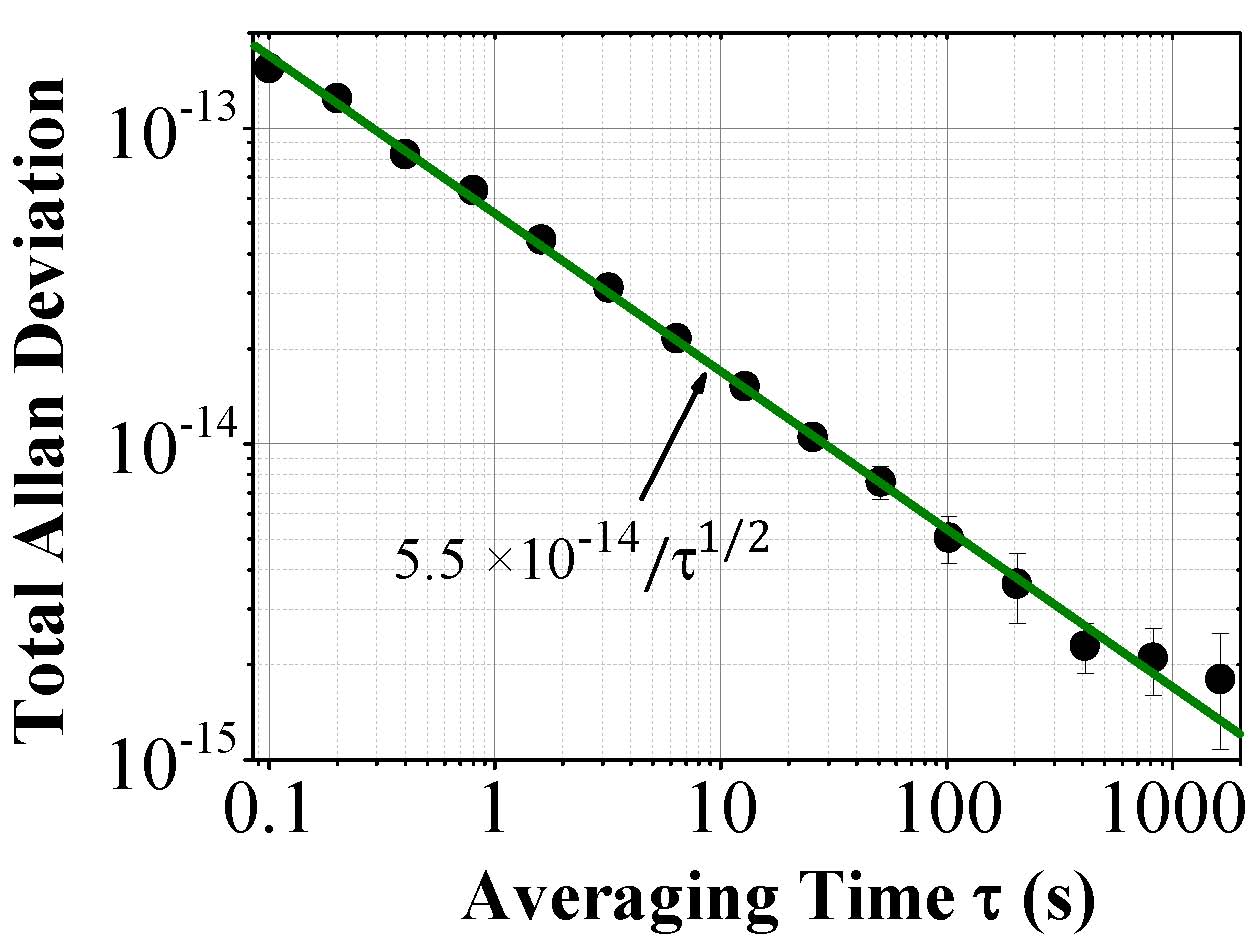
图 4 基于全密封钙束管的小型钙原子束光学频率标准稳定度
接下来我们小组将仍致力于小型化钙原子光钟的研究,主要包括进一步提高系统的稳定度和集成小型化系统,其秒级稳定度理论预计能进入10-16量级[8,9], 而通过对光学部分和电学部分进行集成化可实现集成小型化的系统,使光钟真正实现性能指标好、对环境适应性强、应用范围广的特性。
3.小型铷原子光钟方案
传统的铷原子钟主要是工作在微波频段,系统结构简单可靠,但受限于钟跃迁频率,其稳定度很难进入10-14量级水平。利用85Rb基态5S1/2与第二激发态6P3/2之间的跃迁作为钟跃迁,并结合高信噪比的调制转移谱稳频技术和高速环路锁定,直接将420 nm激光输出频率稳定在铷原子的超精细跃迁谱线上,实现将传统的铷原子微波钟拓展到铷原子光钟。通过自评估的方法,得到该系统的秒级稳定度为1.6×10-14,接近微波钟的量子极限,与目前国际上最好的532nm碘分子光频标性能相当。
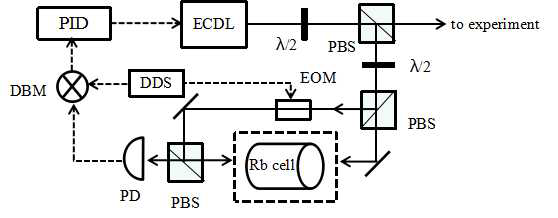
图 5 小型铷原子光钟原理图
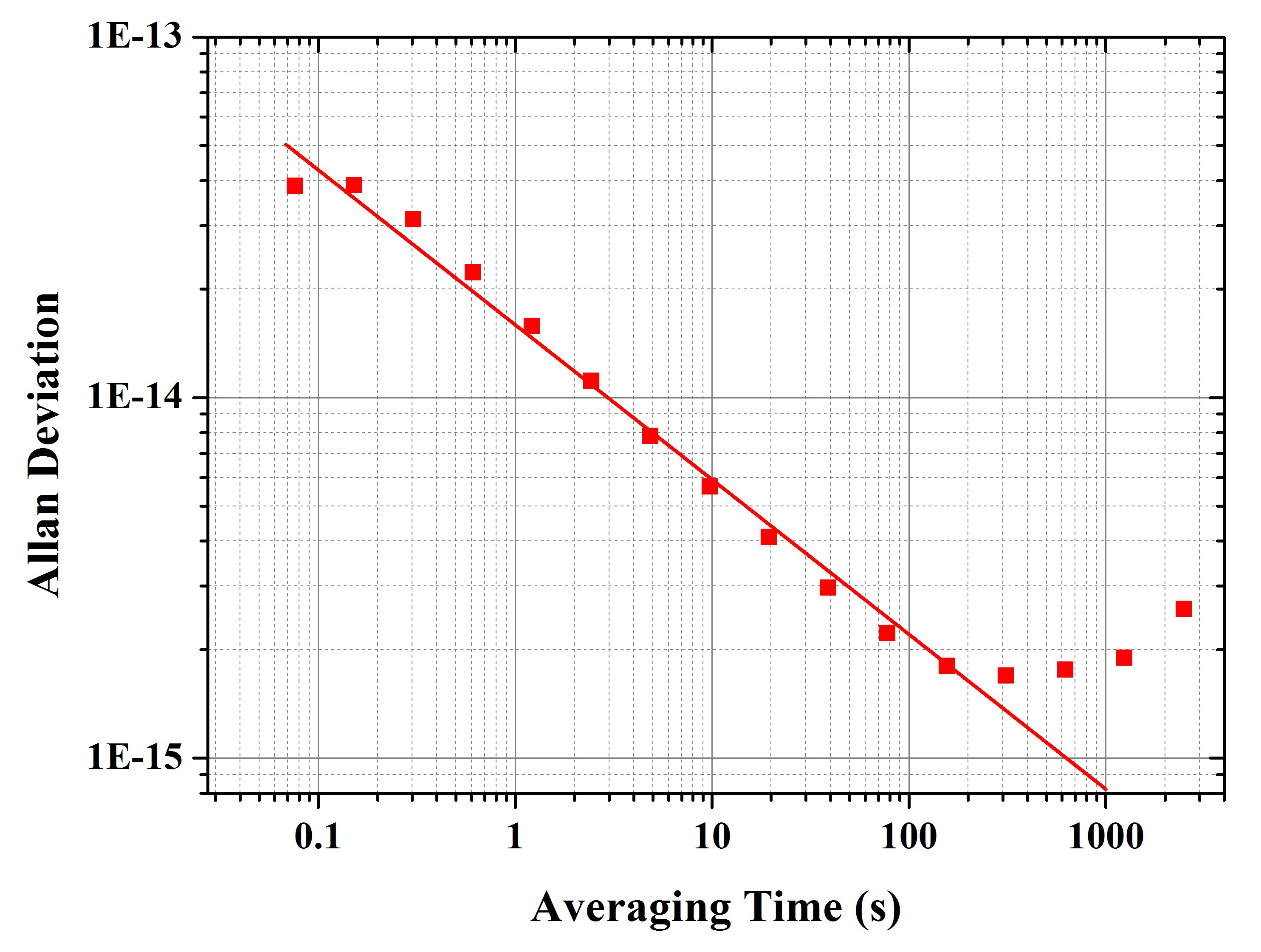
图 6 铷原子小光钟稳定度结果
参考文献:
[1] S. L. Campbell,R. B. Hutson, G. E. Marti, A. Goban, N. Darkwah Oppong, R. L. McNally, L. Sonderhouse, J. M. Robinson, W. Zhang, B. J. Bloom, J. Ye, "A Fermi-degenerate three-dimensional optical lattice clock", Science 358, 90-94 (2017)
[2] T. Takano, M. Takamoto, I. Ushijima, N. Ohmae, T. Akatsuka, A. Yamaguchi, Y. Kuroishi, H. Munekane, B. Miyahara, and H. Katori, "Geopotential measurements with synchronously linked optical lattice clocks," Nat. Photonics 10(10), 662-666 (2016).
[3] S. Kolkowitz, I. Pikovski, N. Langellier, M. D. Lukin, R. L. Walsworth, and J. Ye, "Gravitational wave detection with optical lattice clocks," Physics Review D 94(12), 124043 (2016).
[4] P. Kersten, F. Mensing, U. Sterr, and F. Riehle, "A transportable optical calcium frequency standard," Applied Physics B68(1), 27-38 (1999).
[5] K. Huang, J. Zhang, D. Yu, Z. Chen, W. Zhuang, and J. Chen, "Application of electron-shelving detection via 423 nm transition in calcium-beam optical frequency standard," Chinese Phys. Lett. 23(12), 3198-3201 (2006).
[6] J. J. Mcferran and A. N. Luiten, "Fractional frequency instability in the 10-14 range with a thermal beam optical frequency reference," Journal of Optical Society of American B 27(2), 277-285 (2010).
[7] X. Zhang, S. Zhang, Z. Jiang, M. Li, H. Shang, F. Meng, W. Zhuang, A. Wang, and J. Chen, "A transportable calcium atomic beam optical clock," in Proceedings of IEEE International Frequency Control Symposium (IEEE, 2016), pp. 1-4.
[8] J. Olson, R. Fox, R. Brown, T. Fortier, T. Sheerin, R. Stoner, C. W. Oates, and A. D. Ludlow, "High-stability laser using Ramsey-Borde interferometry," in Proceedings of IEEE International Frequency Control Symposium (IEEE, 2017), pp. 32-33.
[9] H. Shang, X. Zhang, S. Zhang, D. Pan, H. Chen, J. Chen, "Miniaturized calcium beam optical frequency standard using fully sealed vacuum tube with 10-15 instability," Opt. Express 25(24), 30459-30467 (2017).





