拓扑量子相变和量子磁性模拟是当今超冷原子物理领域的前沿研究。在绝对零度下改变多粒子系统的某一参数, 如粒子间的耦合强度、压力或外加磁场强度, 可以将系统从一种有序状态连续变化到另一种有序状态。由于在临界点附近热力学涨落和量子涨落同等重要, 这类相变与仅由温度所引起的热力学相变完全不同, 被称为量子相变。但是在绝对零度下，一个量子系统可能还存在另外一种量子相变，这种量子相变过程并不存在朗道理论的自发对称破缺, 其行为是由系统基态波函数的整体性质决定的，系统在相变点两边均处于无序相之中, 也不存在描述和区分这两个相的定域的序参量，但可能存在非定域的序参量，这类相变我们称之为拓扑量子相变[1]。例如在分数量子霍耳效应中, 电导量子平台之间的相变就是一个典型的拓扑量子相变。

然而，要操控量子相变的参量在凝聚态物理中是十分困难的，我们可以利用光晶格中的量子气体实现这种操控，从而研究量子相变的机理以及发现新的量子相变与实现新的物态。

 

图1 非零温下的量子相图

对于光晶格中的双组份玻色子或费米子，通过赝自旋变量↑和↓以及相互作用ex的+(-)号代表费米子或者玻色子的情况[2]，并因此使系统趋于反铁磁(铁磁)序的相。

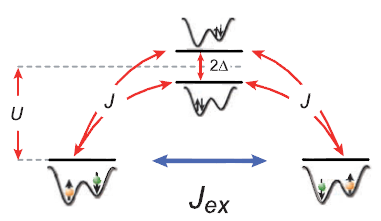
图2 超交换相互作用原理图[3]

        超交换相互作用是形成强关联电子介质中量子磁性的基础，对相邻格点等效自旋-自旋相互作用的控制也成为量子磁性模拟的新途径。这种相互作用是粒子向相邻格点“虚”跳跃的结果：一个粒子跳跃到相邻格点的同时，一个相同粒子（或者相邻格点中的粒子）跳跃回到它原来所在的格点[4]。对于双自旋极化的费米子，这样的跳跃受到泡利不相容原理的抑制，因此具有相反自旋的两个粒子可以产生跳跃并引起粒子总能量的降低。

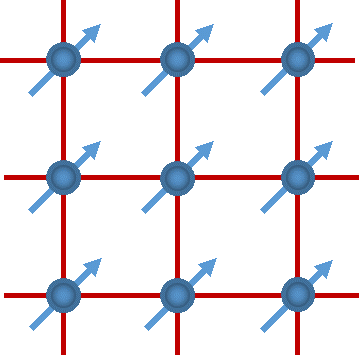
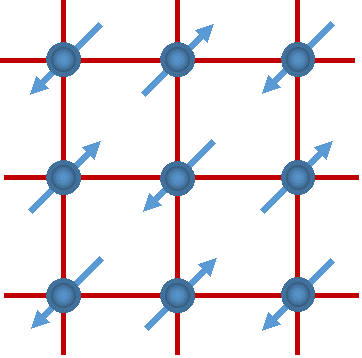
图3 铁磁序                                         图4 反铁磁序

光学晶格中的超冷量子气体

      光晶格是由一对相向传播的相干激光干涉形成的周期性光学势阱，势阱周期等于形成光晶格的激光的波长的一半。在光晶格势阱中，由于ACStark效应产生的光偶极力作用，可以把原子囚禁在光强最强处或最弱处：如果光晶格激光的频率相对于特定的原子跃迁为红失谐，原子就被光晶格囚禁在光强最强处；如果光晶格激光的频率相对于特定原子跃迁为蓝失谐，则原子会被囚禁在光强最弱处。

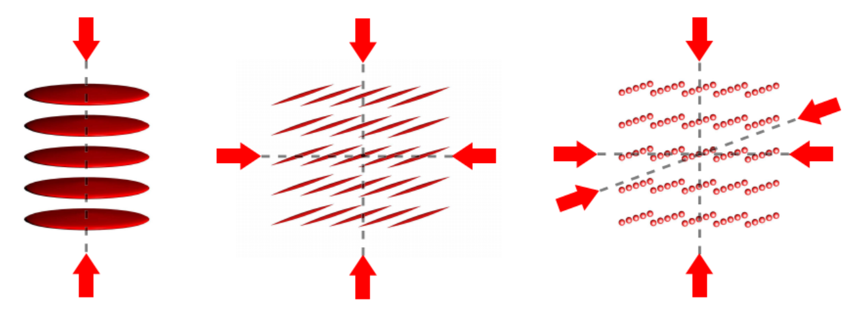
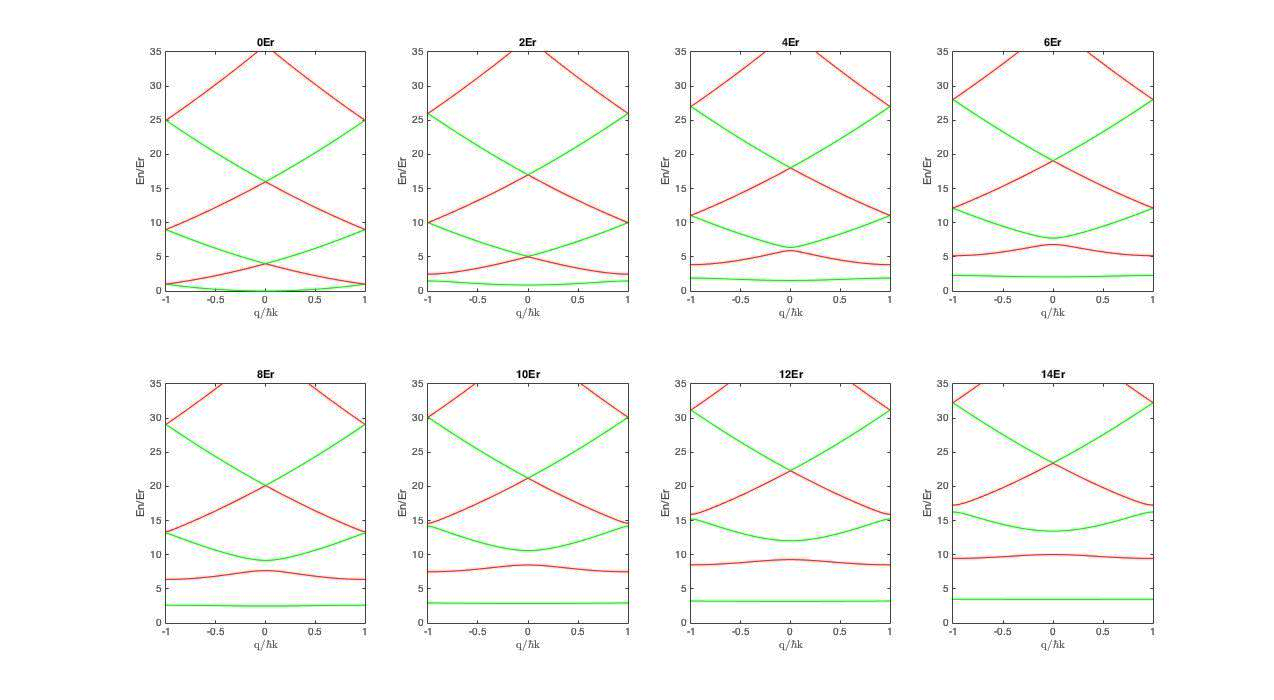
      有关光晶格中超冷原子研究的一个重要原因是其与固态系统的相似性，通过对原子种类和晶格间距的适当选择，我们可以在一个相对可控的实验条件下模拟出多体系统中许多难以达到的条件，进而对凝聚态物理中的相关问题展开探索。例如，通过对Fermi-Hubbard模型的探索和对超交换相互作用动力学机制的研究来尝试给出高温超导问题的答案。

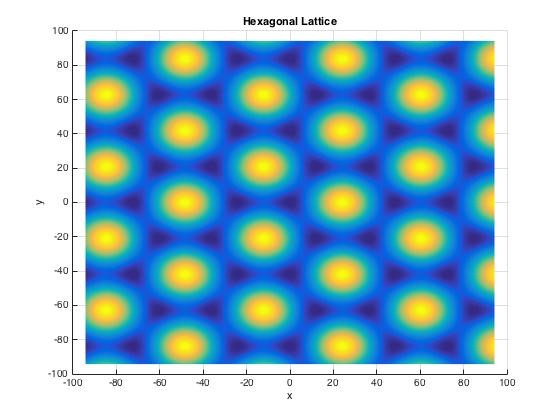
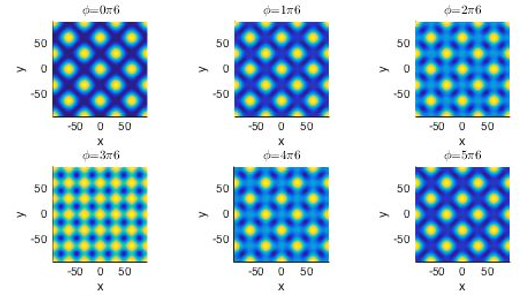
      在实验中，通过对每束光晶格激光光强的全动态控制，我们可以设定特定条件下量子多体系统的相关参数。未来我们准备通过改变光晶格激光的角度和偏振关系来获得其他构型的光晶格结构，以期对更为新奇的拓扑量子相变和更加复杂的量子磁性展开模拟和研究。我们首先通过磁光阱和光偶极阱中强迫蒸发冷却的方法获得30nK的87Rb原子玻色-爱因斯坦凝聚体，然后将凝聚体装载到由三束驻波激光交叠形成的三维光学晶格中。图1是我们在实验上获得的三维光晶格中超流态到Mott绝缘态量子相变的物质波干涉图样，图2是利用一维玻色气体形成的量子牛顿摆。

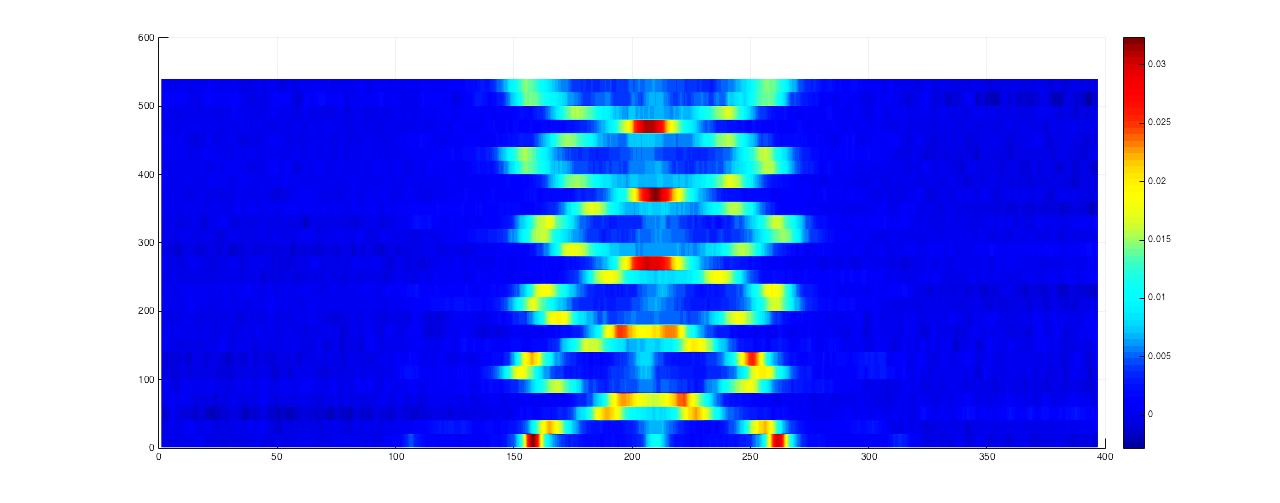
实验系统概述

      整体实验包含真空系统、激光系统、磁场系统、成像系统以及时序控制系统。实验真空系统包括科学腔、二维磁光阱、原子源、离子泵等部分，如下图所示。科学腔真空度为3×10-9Pa，二维磁光阱腔体内真空度为3×10-7Pa。科学腔为鼓形，包括8个2.75英寸窗口、16个1.33英寸窗口以及上下2个8英寸窗口用于通光，其中上下窗口贴近腔体中心位置，为今后实验实现原位探测提供较大的数值孔径。

      中性87Rb原子共有87个核子和37个核外电子，是复合玻色子，自然丰度为27.8%（另外一种稳定的同位素85Rb约占72.2%），原子核半衰期4.88×1010年，通常条件可以认为是稳定的。

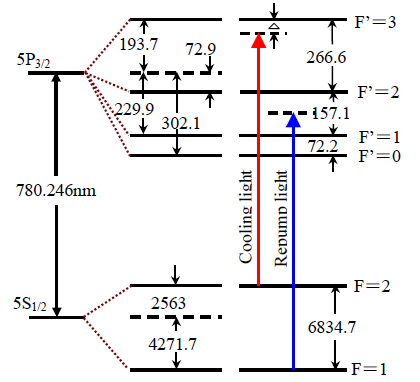
      87Rb原子的核自旋I＝3/2，基态52S1/2分裂为两个超精细能级，分别为F＝1 和F＝2，它们之间的分裂间距为6.835GHz，被用来作为铷原子频标的工作频率；第一激发态52P3/2分裂为F＝0，1，2，3四个超精细能级。它们之间的跃迁被称为87Rb原子的D2线跃迁，图8显示了87Rb原子D2线超精细结构的细节，并标注了搭建激光冷却实验系统的激光中心频率，图中能级分裂单位是MHz。图13是实验激光系统的实物图。

      光偶极阱是由光场与原子的偶极矩相互作用而产生的，典型的深度为毫开尔文以下。由于产生光偶极阱的激光通常情况下都是远失谐激光，因此原子在光偶极阱中被激发的概率非常低，可以很好的用于囚禁中性原子，并进一步通过蒸发冷却的方法快速获得玻色-爱因斯坦凝聚体。