北京大学量子电子学研究所的复杂晶格玻色小组,是我国最早开展铷原子玻色-爱因斯坦凝聚态(BEC)研究的团队之一。当前聚焦于光晶格中超冷玻色气体的动力学研究,通过精密调控手段探索三六晶格系统、晃动晶格中的高能带动力学、跨维度相变等复杂现象,主要研究方向包括:光晶格体系的多维量子相变与关联效应、低维与分数维冷原子气体的新奇量子态与新奇量子特性、高能带动力学及维度调控机制、超冷原子系统中的非平衡态物理与拓扑效应等。通过量子模拟揭示复杂量子体系的演化规律,探索量子物质中新奇的量子效应,为凝聚态物理、拓扑量子物理、量子信息科学及量子计算技术提供实验与理论支撑。
近期主要工作:
• 三重向列相超流体的实现
我们在一种蜂窝状的光晶格中观测到了超冷原子在保持晶格平移不变性的情况下形成破缺晶格转动对称性的超流体,并将此新型量子物质状态命名为三重向列序超流。实验中的一项关键量子调控技术是将超冷原子快速装载到蜂窝状光晶格的高激发能带上。我们通过对激光光场的高精度快速控制,在光晶格高轨道自由度的量子调控方面取得突破,成功制备了蜂窝状光晶格中的高能带凝聚体。基于这种新型的量子模拟平台,实验发现系统会自发形成三重向列序超流体。同时,通过场论重整化的理论分析,发现高能带凝聚体与传统的凝聚体存在重要的不同点。高能带凝聚体中存在显著的多体相互作用重整化,而重整化之后的相互作用导致原子在晶格中倾向于形成空间奇宇称的轨道极化。由场论描述的这种复杂多体效应是向列序超流形成的微观物理机制。
à 相关论文: Phys. Rev. Lett. 126, 035301 (2021)

图1. 左图为三重向列序量子超流体的动量空间分布图;右图为统计分布图。
• 二维电磁力的量子感知技术
我们发展了多项对光晶格中冷原子外态控制的原创技术,可以对数十万原子形成的量子物质波进行高精度的量子调控。实验采用光晶格将物质波的实空间运动和动量空间运动分离开,完成了对量子物质波波矢的控制和测量。同时,物质波在光晶格中的布拉格散射给出了标定物质波波矢大小和方向的精确二维坐标。这种量子测量技术可以直接精确地测量出物质波在力作用下的波矢积累,而不需要测量原子的空间位置变化。该技术通过量子物质波建立了力和普朗克常数之间的直接联系,无需对原子质量、原子数、原子磁矩等物理量进行标定,也就不会受到这些物理量的测量不确定度的影响。实验中量子物质波对力的感知灵敏度达到2E-26 N/√Hz, 突破了上述标准量子极限近一个数量级。团队进行了数千次的量子物质波重复实验,完成了对一个极微弱力的测量,大规模数据的统计分析表明测量精度达到2E-28 N,这个力相当于毫米尺度下原子间范德瓦尔斯力的作用强度。
à 相关论文:Science Bulletin 67, 2291(2022)(封面论文)
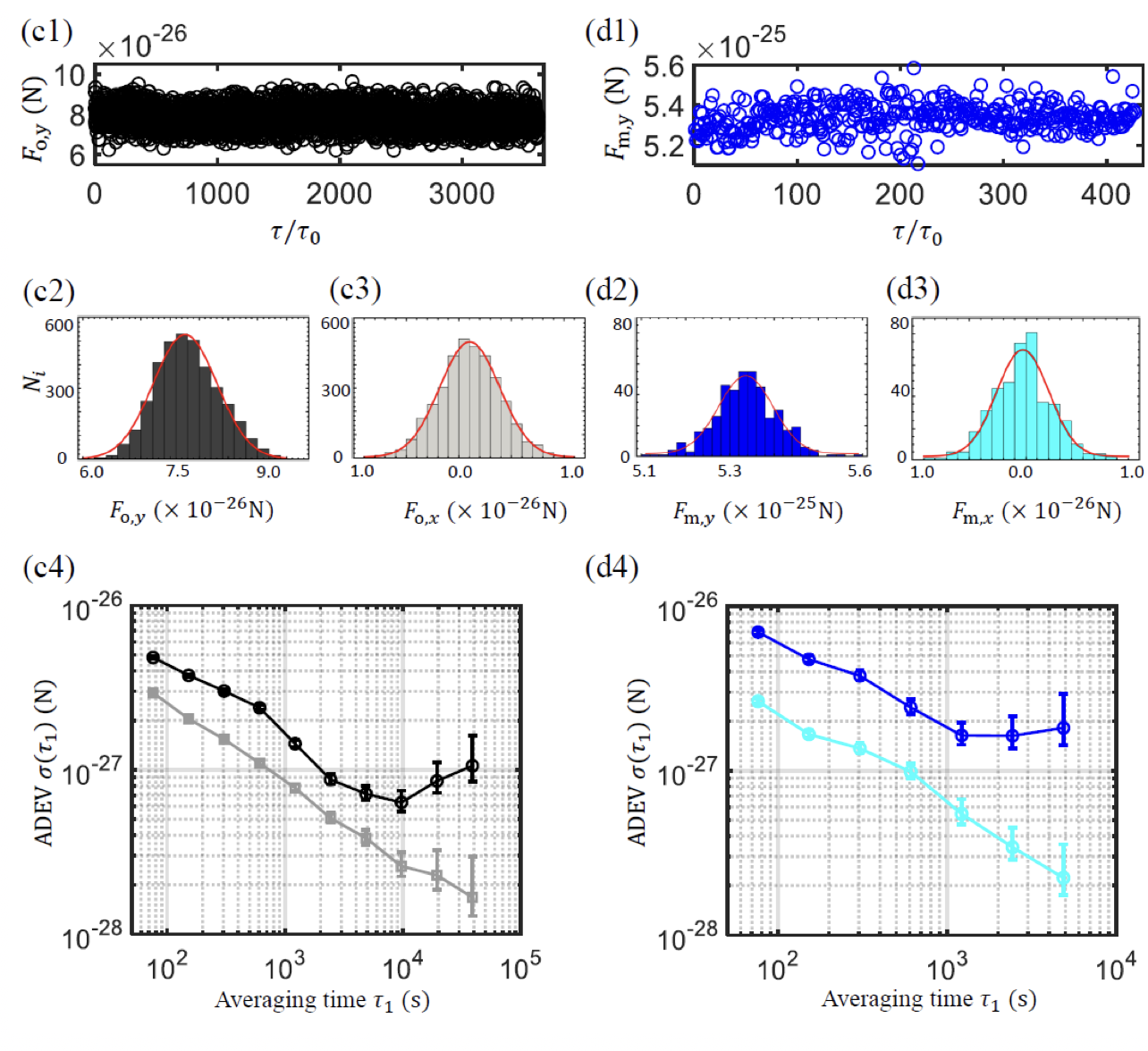
图2 二维电磁力测量结果图。
• 原子轨道的量子门实现
我们在实验上第一次利用一维光晶格的S和D能带将其作为一个量子比特的1态和0态,并在此基础上实现了基于原子轨道的单量子比特非绝热全量子门。实验中,为了保证原子仅在S和D能带上演化,我们利用光晶格阱深幅度晃动的方法,保证实验过程中宇称不变以抑制原子跃迁到P能带,同时通过轨道泄露消除方法,大大降低原子泄露到G能带的概率。最终获得的一系列正弦脉冲序列实现了单量子比特X,Y,Z,H,π/8门,其量子过程平均保真度达98.36%。未来结合单格点操控技术,有望在轨道量子比特上实现任意量子计算。
à 相关论文:Phys. Rev. A 104, L060601 (2021)
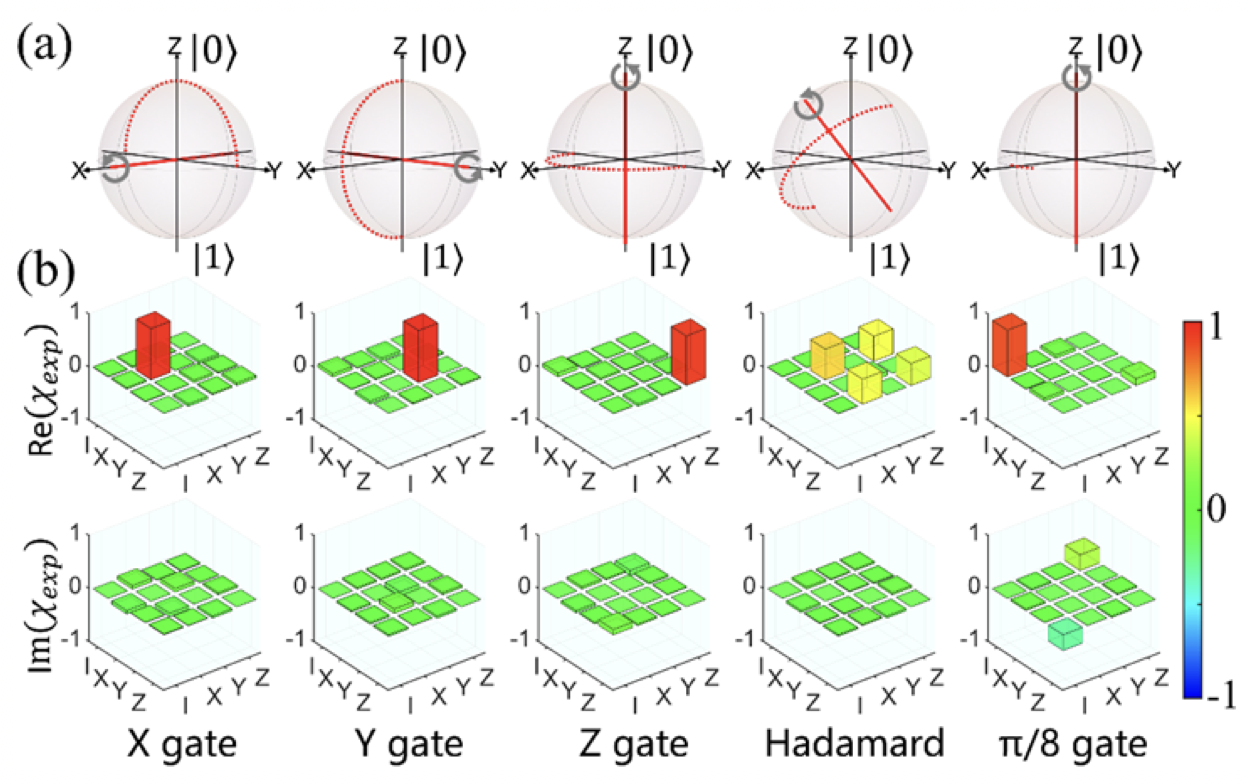
图3 量子门实验结果。(a)量子过程示意图。(b)量子过程层析结果。
• 原子的输运与动力学
在这项实验中,研究了超冷原子在移动光晶格中的传输过程,重点关注S带和D带原子的动力学行为。通过Shortcut方法,超冷原子从玻色-爱因斯坦凝聚态(BEC)快速加载到光晶格高能带中,并通过调节晶格束的相位加速光晶格。这种加速产生了惯性力,导致原子进行布洛赫振荡,D带和S带原子的群速度方向相反。实验中还制备了S带和D带原子的叠加态,通过调节叠加权重实现了原子群速度从正向到负向的调控,并观察到不同带之间的量子干涉效应。
à 相关论文:Phys. Rev. A 107, 023303 (2023)
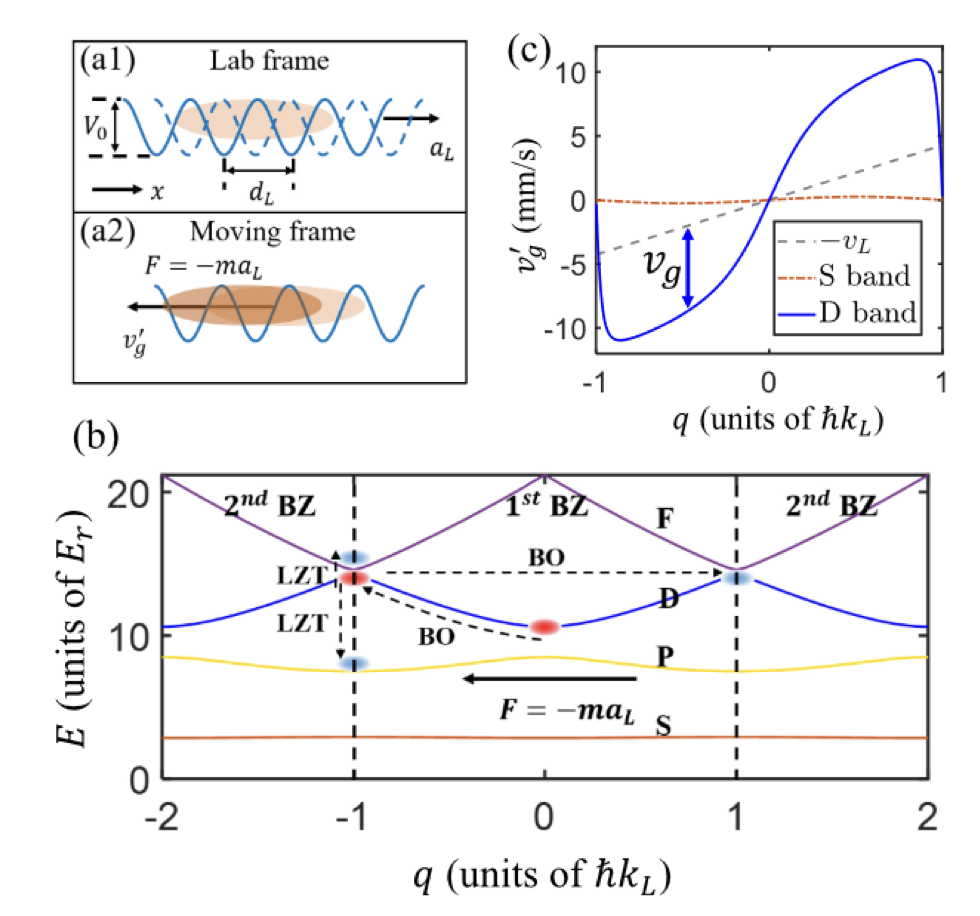
图4:原子在运动光晶格中的输运过程
• 利用原子量子模拟器探索维度交叉的普适相图
我们通过将BEC绝热装载进不同方向可独立调节调的三维三角光晶格中,构建了一个各向异性和温度连续可调的相互作用原子量子模拟器,并探索了维度交叉的普适相图。在低温下,我们确定了从量子三维到零维区域的全相图。通过升高温度,我们观察到不同的量子维度区域随着温度升高而逐渐消失,并发现了一个出现在量子零维和整数维之间的非平凡热态区域。并且,我们展示了量子态-热态跃迁根据维度的不同可分为四种不同的典型普适类,分别为BEC相变、BKT相变、TLL相变与Mott融化。令人惊讶的是,我们还发现了第五种类型,高维量子系统可以通过跨越低维量子区达到热相。其中由于温度升高,热涨落增大导致的系统从高维向低维跨越的过程,我们称为TFDC(thermal fluctuation induced dimensional crossover)。我们的结果为理解非常规维度的射影凝聚态结构提供了重要的基础。
à 相关论文:arXiv:2506.18464

其他代表性论文:
1. Linxiao Niu, Shengjie Jin, Xuzong Chen, Xiaopeng Li, and Xiaoji Zhou.Observation of a Dynamical Sliding Phase Superfluid with P-Band Bosons, Phys. Rev. Lett. 121, 265301 (2018).
2. Tangyou Huang, Zhongcheng Yu, Zhongyi Ni, Xiaoji Zhou, and Xiaopeng Li, “Quantum force sensing by digital twinning of atomic Bose-Einstein condensates,” Communications Physics 7, 172 (2024).
3. P. Tang, X. Dong, W. Zhang, Y. Li, X. Chen, X. Zhou. Implementation of a double-path multimode interferometer using a spinor Bose-Einstein condensate, Phys. Rev. A 101, 013612 (2020).
4. Xinxin Guo, Zhongcheng Yu, Peng Peng, Guoling Yin, Shengjie Jin, Xuzong Chen, and Xiaoji Zhou. Dominant scattering channel induced by two-body collision of D-band atoms in a triangular optical lattice. Phys. Rev. A 104, 033326 (2021).
5. Hongmian Shui, Chi-Kin Lai, Zhongcheng Yu, Jinyuan Tian, Chengyang Wu, Xuzong Chen, and Xiaoji Zhou, Optimal lattice depth on lifetime of D-band ultracold atoms in a triangular optical lattice, Opt. Express 31, 26599-26609 (2023).